미분방정식과 파이썬 패키지

세상 만물과 미분방정식

미분방정식은 변화하는 세상 만물을 엄밀히 표현하는 수학적 언어입니다. 따라서 미분방정식을 컴퓨터로 푸는 일(근사적 해를 찾는 일)은 매우 중요하지요. 흔히 매트랩을 사용하지만, 라이선스가 있는 기관에 소속되지 않은 사람이 쓰기엔 너무 비쌉니다. 그래서 이번 학기부턴 학생들이 파이썬을 활용하도록 유도할 참입니다.

파이썬 패키지

미분방정식과 관련해 파이썬엔 다음과 같은 패키지가 있습니다.

1. scipy.integrate.odeint: 포트란(FORTRAN) 라이브러리인 ODEPACT에 있는 lsoda란 해법을 이용할 수 있게 해 줌.
2. scipy.integrate.ode: (lsoda를 포함한) 여러 종류의 해법을 객체지향적 방식으로 제공.
3. scipy.integrate.solve_ivp: 1, 2보다 나중에 나온 것으로, 2처럼 그러나 2에서완 다르게 (lsoda를 포함한) 여러 종류의 해법을 제공.

1이 널리 쓰여 왔지만, 사용하는 방식은 셋 가운데 가장 덜 파이썬스럽습니다. Lsoda가 훌륭해 그것만 지원한다는 사실은 큰 문제가 아니었고요. 어떻든 파이썬 패키지인 scipy에서도 3을 선택하라는 식으로 권유하고 있기도 해서 테스트를 좀 해봤습니다. Odeint가 결국은 컴파일된 포트란 라이브러리라서 계산 시간이 제일 짧다는 사실은 예상했던 바라, 그건 핵심 논점이 아니었습니다. 또 3의 계산 시간을 줄이는 방법도 있겠다 싶고요. 한데 제가 답을 아는 두 종류(하나는 비선형, 다른 하나는 선형)의 미분방정식에서 1이 오차가 가장 작은 거로 나타났습니다.

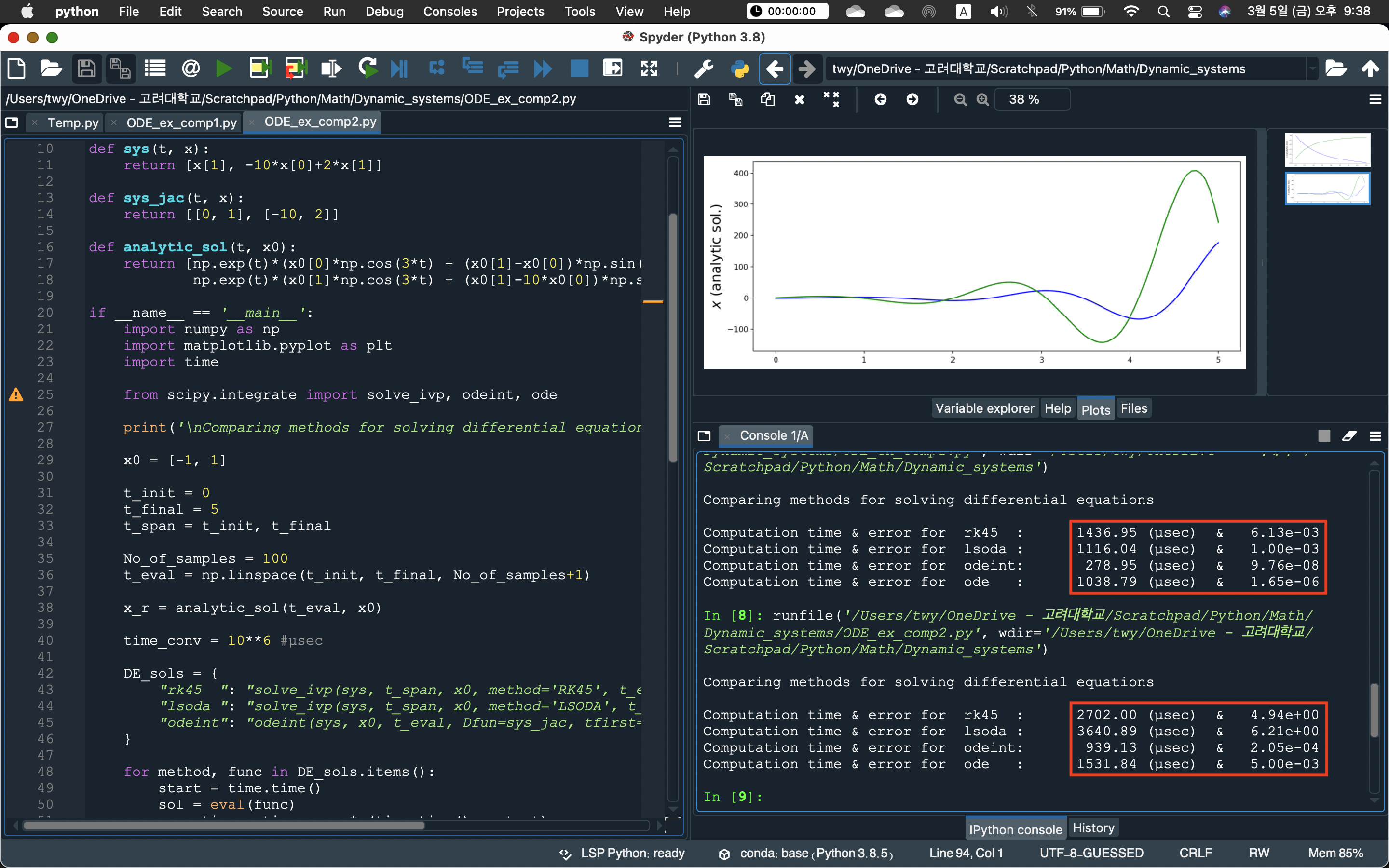
이 그림에서 rk45와 lsoda는 3(solve_ivp), ode는 2에서 lsoda를 선택한 결과입니다. 1은 그냥 odeint라 적었고요. 보시다시피 odeint가 제일 낫습니다. 물론 solve_ivp 같은 알고리즘에서도 rtol이나 atol 같은 파라미터를 기본값(1e-6?)보다 작게 잡으면 오차는 줄어들겠지만, 그만큼 계산 시간은 더 길어질 것입니다.

여전히 odeint!

덜 파이썬스럽거나 말거나 1이 더 정확하기까지 하니 3으로 옮겨갈 이유는 없다고 판단했습니다. 계속 1에 머물자는 게 결론이었지요. 학생들에겐 이런 사정을 설명하며 odeint를 권하기로 합니다.

주의!

미분방정식의 우변이 빠르게 바뀌거나 심지어 불연속적으로 변하는 상태(stiff equation)가 반복되면, odeint는 어려움을 겪을 수 있습니다. 이럴 땐 시간 간격을 좁히거나 mxstep의 값을 크게 잡아주어야 합니다. 그러면 계산 시간이 짧다는 odeint의 장점을 잃게 돼, lsoda 이외의 다른 해법도 함께 제공되는 solve_ivp를 사용하는 편이 더 나을 수 있습니다. 따라서 저의 지침은 이렇습니다.

1. odeint를 사용한다.
2. odeint에서 경고 메시지(warning)가 나오면, solve_ivp를 선택한다.

참고: odeint를 이용한 시뮬레이션 결과는 여기서 보실 수 있습니다.